Bảng đạo hàm đầy đủ và chính xác nhất
Last Updated on January 16, 2023 by
Những bài toán cấp 3 thường có rất nhiều công thức quan trọng và dễ nhầm lẫn, một trong số đó là bảng đạo hàm và đạo hàm lượng giác. Để các học sinh có thể lưu lại công thức và nhớ dễ dàng nhất, chúng tôi sẽ tổng hợp lại bảng đạo hàm, đạo hàm lượng giác, đạo hàm cấp cao,…

Các quy tắc đạo hàm cơ bản
Bảng công thức đạo hàm cơ bản bao gồm: các công thức tính đạo hàm, công thức đạo hàm lượng giác, công thức đạo hàm cấp cao, công thức đạo hàm logarit, công thức tính đạo hàm cấp cao…
Để làm được các bài tập về đạo hàm, điều cơ bản nhất cần phải nhớ chắc chắn phải là các quy tắc đạo hàm cơ bản, đây chính là tiền đề để tạo nên bảng công thức đạo hàm cơ bản và làm các bài tập khó hơn.
(c)′=0(c)′=0 (với c là hằng số)
(uv)′=(u)′v+(v)′u(uv)′=(u)′v+(v)′u
(cu)′=c.(u)′(cu)′=c.(u)′
(uvw)′=u′vw+uv′w+uvw′(uvw)′=u′vw+uv′w+uvw′
(u±v)′=(u)′±(v)′(u±v)′=(u)′±(v)′ (đạo hàm của một tổng bằng tổng các đạo hàm)
(uv)′=(u)′v−(v)′uv2(uv)′=(u)′v−(v)′uv2
(xn)′=n.xn−1(xn)′=n.xn−1 (với n là hằng số tự nhiên)
=> Xem Podcast là gì? Phát hành Podcast như thế nào?
Đạo hàm của hàm hợp
Đạo hàm của một hàm số thực trong giải tích toán học là sự mô tả sự biến thiên của hàm số tại một điểm nào đó. Đạo hàm cùng với tích phân (một phép toán ngược lại), là một trong hai khái niệm cơ bản trong giải tích, giúp cho chúng ta tìm ra con số chính xác nhất cho các kết quả tính toán. Biểu diễn hình học có hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số chính là biểu hiện của đạo hàm.
Để có thể dễ dàng nhớ được, bạn cần phải làm nhiều bài tập liên quan đến các công thức để áp dụng các công thức vào bài tập, và dần dần bạn sẽ sử dụng nhuần nhuyễn các dạng bài, nhớ các công thức lâu hơn.
=> Tìm hiểu Podcast tiếng việt hay nhất
Công thức đạo hàm của hàm hợp là:
Nếu y = y(u(x)) thì y′(x)=y′(u).u′(x)
Bảng đạo hàm nguyên hàm
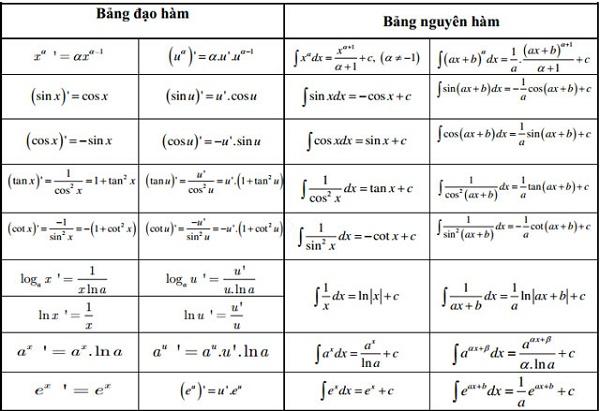
Đạo hàm, nguyên hàm là những kiến thức thường được dạy trong chương trình phổ thông lớp 11 và 12 và cũng thường gặp trong các đề thi tốt nghiệp đại học. Vì vậy, nắm vững bảng đạo hàm nguyên hàm là điều rất cần thiết. Nếu bạn thấy mình vẫn còn hổng kiến thức về bảng công thức đạo hàm nguyên hàm thì bạn nên tham khảo thêm các bài tập trong các sách bài tập, sách nâng cao hoặc bài tập trên mạng để luyện tập thêm.

Bảng đạo hàm nguyên hàm đầy đủ nhất dành cho học sinh cấp 3
Bảng đạo hàm của các hàm số sơ cấp cơ bản gồm hàm số đa thức, phân thức hữu tỉ, hàm số căn bậc hai, lũy thừa, mũ, lôgarit, đạo hàm hàm số lượng giác,…; và các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương; đạo hàm hàm hợp).
=> Tìm hiểu Podcast tiếng anh hay nhất
Tính đạo hàm bằng máy tính như thế nào?
Máy tính cầm tay là một công cụ đắc lực trong việc tính đạo hàm cấp 1, cấp 2. Tính đạo hàm bằng máy tính mang lại kết quả có độ chính xác cao và các thao tác thực hiện rất dễ dàng như sau:
Tính đạo hàm cấp 1:
Tính đạo hàm cấp 2:
Dự đoán công thức đạo hàm bậc n :
+ Bước 1: Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3.
+ Bước 2: Tìm quy luật về số, quy luật về dấu, về hệ số, về biến số, về số mũ rồi rút ra công thức tổng quát.

Bảng đạo hàm lượng giác
Đạo hàm lượng giác xuất hiện rất nhiều trong các đề thi bởi người ra đề có thể khai thác được rất nhiều đề bài từ các công thức trong bảng đạo hàm lượng giác. Dưới đây là bảng đạo hàm lượng giác đầy đủ nhất:

Tính đạo hàm bằng định nghĩa
Sử dụng định nghĩa để kiểm tra sự tồn tại của đạo hàm và tính đạo hàm của hàm số tại một điểm, đây là kiến thức mở đầu của chương đạo hàm tuy nhiên lại rất hay bị các em học sinh lãng quên. Dưới đây là các kiến thức rất quan trọng về tính đạo hàm bằng định nghĩa mà các em cần nhớ để làm các bài thi:
Phương pháp này thường áp dụng đối với giới hạn có dạng limx→x0 f(x)/g(x) limx→x0 f(x)/g(x); trong đó g′(x0)≠0 g′(x0)≠0, g′(x0) g′(x0) tồn tại hữu hạn và f(x0)=g(x0)=0f(x0)=g(x0)=0, tức là dạng giới hạn 0000.
Nếu giới hạn limx→x0 f(x)/g(x) limx→x0 f(x)/g(x) thỏa mãn các điều kiện trên thì phương pháp này rất có hiệu quả và dễ thực hiện hơn nhiều so với các phương pháp bình thường như : phương pháp thêm bớt hạng tử, dùng biểu thức liên hợp, sử dụng các giới hạn lượng giác cơ bản.
=> Chia tay những kỷ niệm thời học sinh ở đây
Đạo hàm cấp cao
Giả sử hàm số y = f(x) có đạo hàm f'(x)
Đạo hàm của hàm số f'(x), nếu có, được gọi là đạo hàm cấp hai của hàm số f(x), kí hiệu là y” hay f”(x).
Đạo hàm của hàm số f”(x), nếu có, được gọi là đạo hàm cấp ba của hàm số f(x), kí hiệu là y”’ hay f”'(x).
Tương tự, đạo hàm của đạo hàm cấp (n-1) được gọi là đạo hàm cấp n của hàm số y = f(x), kí hiệu là y(n)hay f(n)(x).
f(n)(x)=[f(n−1)(x)]′f(n)(x)=[f(n−1)(x)]′ , với n thuộc Z và n >= 2
Bảng đạo hàm cấp cao đầy đủ và công thức Lepnit:

Bảng đạo hàm cơ bản và bảng đạo hàm mở rộng sẽ là kiến thức nền tảng trong chương trình toán học THPT mà sẽ theo chân bạn từ ghế nhà trường cho đến những kì thi tốt nghiệp và sau đó là đại học. Bước qua những kỳ thi trên nó sẽ tiếp tục đồng hành với các bạn trong chương trình toán cao cấp mà bạn sẽ học ở môi trường đại học. Vì vậy, để làm được các bạn tập đạo hàm, bạn cần thuộc hết các công thức đạo hàm cơ bản và sơ cấp sau đó sẽ còn nâng cao lên trong môi trường đại học.
=> Ứng dụng của 5 kim loại cứng nhất hành tinh

Trên đây là những kiến thức về đạo hàm căn bản và vô cùng quan trong đối với các em học sinh chuẩn bị cho các kỳ thi kể cả đại học. Vì toán học biết rằng nói dài dòng lý thuyết sẽ không giúp được gì nhiều trong cách giải bài tập, nên để có thể nhớ hết các công thức thì các em nên viết các công thức đạo hàm ra giấy nhớ và dán vào những nơi mà mình dễ nhìn thấy nhất để dễ dàng học thuộc.
Mong rằng những tổng hợp về bảng các công thức đạo hàm quan trọng trên đây sẽ giúp bạn có một kho lý thuyết đầu đủ và chi tiết để có thể áp dụng làm các bài tập về đạo hàm và có một kết quả tốt trong các kỳ thi.
